This article has been written by Lisa A.
In this article, we explore auctions in general and their application and significance in blockchain in particular. We start the context of auction evolution from the first one documented in a written form up to its application in blockchain. We then provide some basic definitions to make it easier to grab further explanations and a range of auction types starting with the most well-known like English and Dutch auctions and going to the more exotic ones like Gradual Dutch Auction, Combinatorial Auction, or EIP-1559.
After that, we briefly cover the auction explanation provided by the Auction Theory and then explore the same question from the Mechanism Design perspective. In the end, we use the EIP-1559 case and its possible alternatives as an example of advocating for a specific auction design and proving its soundness.
Contents
-
Context
-
Definitions
-
Auction types
-
Types
-
More fun: other types to consider
-
-
What is an auction from the Auction Theory Perspective
-
What is an auction from the Mechanism Design Perspective
-
Auction design specific example: EIP-1559
-
Sources
Context
Disclaimer: the section “Context” provides a very brief history of auctions and some intuition behind their evolution. Feel free to skip, and go to the section “Types” if you are interested in purely practical explanations.
Auctions have existed for a pretty long time. Around 500 BC, the Greek historian Herodotus was the first to mention the auction procedure, reporting that it was used in Babylon to sell women for marriage.
-
Before the phone and internet era, auctions took place in offline venues. People gathered at a specific time at a specific place and conducted an auction. Auctions were used to allocate almost anything (fish, pieces of art, financial assets, slaves, wife, real estate, debt, etc.) One of the most famous offline “old school” auction type was “candle auction.” In a candle auction, the end of the auction was signaled by the expiration of a candle flame, which was intended to ensure that no one could know exactly when the auction would end and make a last-second bid.
-
With the beginning of the “Internet era”, we see the appearance and wide adoption of internet auctions. They added flexibility to auctions that existed before as it’s just much more convenient to conduct an auction online without any geographical constraints. An example of convenience adoption was eBay – that allowed to sell whatever you want to the highest bidder.
-
Internet also introduced a range of new use cases, such as ad auctions used by Google, Facebook, and many other advertising platforms. With the dawn of social networks and “big data” (personal data collection and analytics), the phenomenon of “targeted ads” appeared. That is, the advertisers could now choose dozens of characteristics of their target audience. That introduced a very new auction type, “bidding on a category” (i.e. the auction for ad placement for a specific, narrow audience.) This type of auction differs from for example trading auctions. As there are very few auctions that are active at any particular time because there's only like certain cohorts that are using the product. One calls such type of auctions “sparse” auctions. Furthermore, people don’t bid. Instead, the platform (e.g., Google) executes your strategy for you.
-
With blockchain, auctions got a new boost of research and development as the domain has its own specifics. For example, if the “traditional” stock exchange market has its opening and closing time, that is, in blockchain, auctions don’t stop, that is, there is no such phenomenon as opening and closing price. Furthermore, in a blockchain environment, each on-chain operations costs money so the auction might be pretty expensive so it is crucial to minimize its complexity.
Some examples of auctions in blockchain include
-
Transaction fees. As the “first precedent” in blockchain, a first price auction was proposed in the Bitcoin paper to sell the block space in the market. That is, the transaction fees are exactly bids on an auction which sells Bitcoin’s blockspace.
-
In ICO times (2017), auction was a tool to start a new market around a new coin.
-
Auctions were also used for NFTs as a tool to allocate a scarce good.
-
MEV extraction (except the regular transaction fees) can be a certain type of auction (if using the Proposer-Builder Separation (PBS) environment). It was firstly introduced by Flashbots to kind of reduce spam on Ethereum (in particular, in case of gas wars when several parties bid against each other to gain a more favourable position in the block) by basically having people bid in an auction off-chain instead of spamming the validators to insert transactions on-chain. Then the validators agree to the outcome of that auction. In MEV auctions, one bids on sequences not a single transaction inclusion (like in EIP-1559).
-
Internet and blockchain boosted the R&D around auctions as more narrow use cases required more specific auction solutions. The 2020 Nobel Prize for Economics was awarded to Paul R. Milgrom and Robert B. Wilson “for improvements to auction theory and inventions of new auction formats.”
Definitions
Below are some auctions affiliated definitions that will help to understand the auction descriptions in the next sections.
-
Credible auctions – auctions where you do not need to trust the auctioneer. It's a very different take from traditional economics because often you assume the auctioneer is honest but in practice auctioneers might actually try to manipulate their auction to increase revenue.
-
Dynamic auction – bidding takes place over several rounds.
-
Incentive design – designing a system or institution according to the alignment of individual and user incentives with the goals of the system. In case of auctions, it should take in the account if the buyers have an incentive to report their truthful valuation, if the auctioneer has an incentive to be honest, etc.
-
Opening price – the price at which an asset first trades upon the opening of an exchange on a trading day.
-
Closing price – the last price at which an asset trades during a trading day.
-
Public auctions – all the bids are public.
-
Private auctions - the bidders submit bids to the auctioneer in a sealed kind of format.
-
Truthful revelation – an equilibrium in which the seller and all the bidders get the same expected utilities. It is also often referred as an equivalent direct revelation mechanism.
-
Revelation – how participants in an auction reveal their preferences. It can be direct revelation, when the participants are asked explicitly “What are your preferences?” and indirect revelation, when the participants are asked about their preferences in a more fancy and vague way as they might have an incentive to report false preferences if asked directly.
-
Off-chain agreements – buyers colluding with each other (for example to make the supply scarce by buying as a group) or seller colluding with a buyer.
-
Reserve price (1) – a minimum price that a seller would be willing to accept from a buyer. It can be either disclosed by the seller or not.
-
Reserve price (2) – a fixed payment allowing to enter the auction.
Types
Disclaimer: type descriptions are informal and aimed at just providing the intuition behind the working mechanisms.
Auctions differ by several criterion such as ascending or descending price, buyers bid or sellers bid, bids are revealed or not, one round or more,
Basics of auction types
English and Dutch auctions are kind of the antipodes of each other.
-
English Auction – someone bids, someone else bids more, and so on until no one is willing to bid higher.
-
Dutch Auction – the auctioneer starts with the highest asking price and lowers it until someone is ready to buy the item.
-
Sealed-Bid Auction – all bidders simultaneously submit sealed bids to the auctioneer so that no bidder knows how much the other auction participants have bid.
-
Open-bid Auction – bidders make bids openly and everyone can observe the bids of the others.
-
First-Price Auction – the winner pays the exact bid they did.
-
Second-Price Auction – the highest bidder wins but only pays the price equal to the second-highest bid plus one cent.
-
Private Value Auction – the bidder only knows their own value of the item (relevant for items with subjective value like artworks).
-
Common Value Auction – the value of the item is the same for everybody (relevant for items with objective value like oil fields).
More fun: other types to consider
Disclaimer: this section includes both pretty widely known auctions and less known auctions as the aim of this section is to highlight different types and mechanics.
-
Vickrey Auction – second-price sealed-bid auction.
-
Third-price auction – similar to the second-price auction but the winner pays the third highest bid.
-
Gradual Dutch Auction – a sequence of auctions that are started one at a period of time. The price of each auction is going down as that of a Dutch auction. The starting price of each new auction in the sequence is based on the trades in the previous auction.
-
All-pay auction – all bidding participants pay their bid amount, regardless of whether they have placed the highest bid.
-
Reverse Dutch Auction – the opposite image of the forward (classical) Dutch Auction. The buyer defines artificial low starting price, at a point where the offer is believed to be zero. At specific intervals, the price is rising and continues to rise until the supplier is ready to make an offer.
-
Reverse Auction – sellers bid for the prices at which they are willing to sell their goods and services. It is the opposite of a regular auction, where a seller puts up an item and buyers place bids.
-
Double auction – buyers and sellers submit bids and offers. Bids tend to increase, and at the same time, offers tend to decrease.
-
Combinatorial Auction – participants can place bids on combinations of different items, or “packages”, rather than individual items.
-
Deferred Revelation Auction – a two-phase auction consisting of a commitment and a revelation phase. During the commitment phase, each buyer sends a cryptographic commitment to a bid to the auctioneer. The auctioneer is responsible for sharing the cryptographic commitment with all other buyers. During the revelation phase, each buyer reveals their bid. Finally, the auctioneer implements the second-price auction with reserves with the revealed bids. To punish a buyer that refuses to reveal their bid, each buyer must also deposit collateral during the commitment phase which is refunded only if their bid is revealed.
-
Japanese Auction – a type of English auction. No new bidders are allowed to join once the bidding starts. The price of the item in the auction keeps increasing during the bidding process. The bidders who do not want to keep up with the auction price are free to drop out. The process ends when one bidder remains.
-
Chinese Auction – a type of the all-pay auction, where the probability of winning depends on the relative size of a participant's bid.
-
EIP-1559 Auction – This type of auction can be seen as an AMM (Automated Market Maker) where a protocol sells a limited resource, and where transactions buy up the right to use that resource (increasing its price) while the protocol sells the resource at a rate that is deemed sustainable. This ensures that the use of the resource is bounded (its price keeps increasing if demand is higher than the supply) while also ensuring a fair price is paid for the resource for a given time period.
What is an auction from the Auction Theory Perspective
Auction components
-
Number of bidders n, .
-
Single item to be sold. Note: multiple items auctions exist as well but they are out of the scope of this article.
-
Signal , that is, each bidder gets some signal about the value of the item. For example in case of an artwork, the valuation can be provided by some external expert. .
-
The signal is distributed according to some probability distribution , that is, in our example of an artwork, the distribution will cover all the valuations that could be provided by other experts and could be picked as . We write ~ . is continuous with a pdf (probability density function) .
-
We assume that (i) all bidders drew their signals the same distribution function, (ii) all the signals are independent. We can write is independent of for any .
-
The value of the item . In case of the private value auction, . But in case of the common value auction, it might differ.
-
The utility function of each bidder . For example, in the first-price auction, . And in the second-price auction, if for all j ≠ i, where are the bids of all other bidders except for bidder and otherwise.
As a side note: utility describes the benefits gained or satisfaction experienced with the consumption of goods or services. Utility function measures the preferences consumers apply to their consumption of goods and services.
-
An allocation rule – answers the question “who wins?”
-
A payment rule – answers the question “Who makes the payment and how much?”
-
An equilibrium concept such as Bayesian Nash Equilibrium or Dominant Strategy Equilibrium. As a side note: equilibrium is a state in which no player has an incentive to change their strategy.
-
Risk preferences of bidders, such as risk-neutral, risk-averse, and risk-acceptant.
-
Level of information available, such as complete or incomplete information.
-
Bidder’s strategy – the options which they choose in a setting where the optimal outcome depends not only on their own actions but on the actions of others. For example, in the second-price auction, it’s a weakly dominant strategy for all bidders to bid their true value, that is for all . While in the first-price auction, the dominant strategy for all bidders is to bid less than their true value.
Building an auction
Out of these components, one is ready to build an auction. The specific design depends on the following criterion:
-
What is the objective? Revenue maximization, efficiency maximization, or something else. If the objective is revenue maximization (that is pretty reasonable for an auction), then, under certain assumptions (risk-neutrality and individual private value), there is no difference between first-price auction, second-price auction, third-price auction, and even all-pay auction, as the expected revenue in all of them will be the same (the reasoning is outside the scope of this article, but if you are curious, check the “Auction Theory” section in the Advanced Game Theory course by Selcuk Ozyurt.)
-
However, if these “certain assumptions” are not the case, the analysis is more complex and one should consider risk preferences, correlated values, collusion, entry deterrence, reserve price, etc.
-
According to the Auction Theory:
-
For correlated values, ascending auctions work better.
-
For risk-averse bidders, there is no difference between the first-price auction and the second-price auction. However, the bidding strategies will be different.
-
To mitigate the collusion, sealed-bid auctions makes a lot of sense.
-
In case of entry deterrence, sealed-bid auctions work better to promote entry.
-
Sometimes hybrid format auctions make sense, such as Anglo-Dutch auction. That is, unless the number of participants is bigger than two, they play an ascending auction. When there are only two bidders left, they play the first-price auction.
-
What is an auction from the Mechanism Design Perspective
Mechanism design helps people to build and design games. In our case, we can engage it into designing auctions that will reach pre-determined objectives given a specific environment.
While thinking about designing a mechanism, the “mechanism designer” considers the following objectives.
To describe an auction from the Mechanism Design perspective, we first need to describe what is a mechanism.
What is a mechanism and generalized Mechanism Design setting
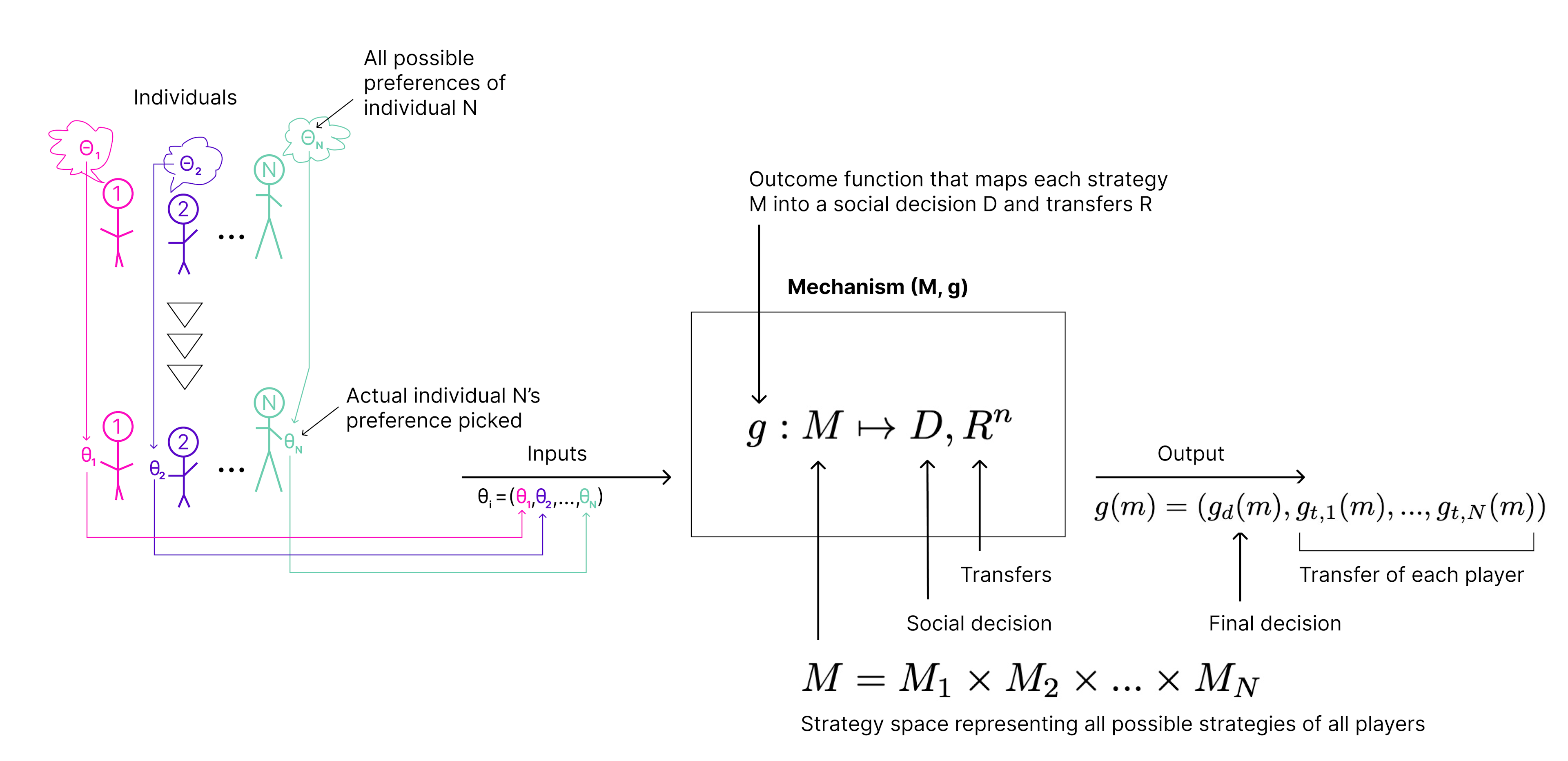
-
Individuals where .
-
The set of all potential social decisions where can be finite or infinite.
-
The set of all possible player types where individual i’s information (private input) is represented by their type where .
-
Individual i’s utility function where is a real number. means that the individual $i $ prefers decision over given that their type is .
-
Decision rule is a function that maps each type profile into a decision .
-
Decision rule is efficient if for all $i = 1, …, n, $ , and . That is, the decision rule is maximizing the total sum of agents’ utilities. In other words, no individual can be better off without making someone else worse off.
-
Transfer function is a vector of size ) where represents the payment that $i $ based on the reported types can be greater than zero meaning that an individual i receives a payment or the opposite. Transfer function is an optional component. For example, in an auction mechanism, there is a transfer function, while in the voting mechanism there is no transfer function.
-
Social choice function where is the decision rule and is the transfer function.
-
Received utility where is the announced vector of types and is the i’s true type.
-
The transfer function is feasible if for all and . The transfer function is balanced if for all and .
-
A mechanism is a simultaneous move game. Formally, mechanism is a pair (, ) where is a strategy (or message) space representing all possible strategies of all players and is an outcome function that maps each strategy into a social decision and transfers . That is, . Thus, for each , the function represents the final decision and transfers where is the final decision and are the transfers of each player.
When we have a defined game, that is, we fixed all the elements mentioned above, we want to predict the game outcome. To do this, we use one of equilibrium mechanisms such as Dominant Strategy Mechanism.
-
Dominant strategy means that whatever other players play, playing the strategy gives the highest possible pay-off. Formally, the strategy is dominant if the utility of playing this strategy is larger or equal than the utility of playing any other strategy: for all and where is the dominant strategy.
-
A social choice function is implemented in dominant strategies if the social choice function and the outcome function have the same outcomes for all players. Formally, a social choice function is implemented in dominant strategies by the mechanism (,) if there exists function such that is a dominant strategy for all and and for all .
Example of auction as a mechanism (Vickrey Auction)
-
Single object to auction.
-
individuals are bidders.
-
Decision for all . That is, equals 1 if the individual wins and 0 otherwise. But there is exactly one individual who wins.
-
Player type is represented by their valuation of the object: .
-
The efficient decision rule, by definition, says that the item should be allocated to the individual who values it at most. That is, for any and , if for any and otherwise.
-
The transfer function is the payment that the winner makes to get the item. If , meaning that if an individual doesn’t win – they do not pay. If , then for any . That is, the transfer is the second highest valuation as prescribed by the rules of the Vickrey Auction.
Auction design specific example: EIP-1559
Disclaimer: this section is based on the paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden. For full experience, check the paper on your own, it’s fantastic.
In this section, we first briefly formalize three desirable game-theoretic guarantees for a transaction fee mechanism, then we will describe how EIP-1559 mechanism works, and in the end we will check how far EIP-1559 satisfies these guarantees compared to the first-price auction used on Ethereum before EIP-1559.
Three desirable game-theoretic guarantees for a transaction fee mechanism
-
The block producers should be incentivized to carry out the mechanism as intended, and strongly disincentivized from including fake transactions.
-
The optimal gas price to specify should be obvious to the creator of a transaction.
-
There should be no way for block producers and users to collude and strictly increase their utility by moving payments off-chain.
Notations and definitions for EIP-1559
-
– the maximum size of a block in gas.
-
– the marginal cost of gas unit to a block producer.
-
– the set of transactions in the mempool at the time of the current block’s creation.
-
– fake transactions. In addition to choosing an allocation, we assume that block producer can costlessly add any number of fake transactions to the mempool.
-
Three parameters associated with each transaction :
-
A gas limit in gas – the maximum amount of gas a tx is allowed to use.
-
A value in gwei per unit of gas – the maximum gas price the transaction’s creator would be willing to pay for its execution in the current block.
-
A bid in gwei per unit of gas – the gas price that the creator actually offers to pay.
-
-
A transaction fee mechanism decides which transactions should be included in the current block, how much the creators of those transaction have to pay, and to whom their payment is directed. These decisions are formalized by three functions: an allocation rule, a payment rule, and a burning rule.
-
A transaction fee mechanism is specified by its allocation, payment, and burning rules. So, a transaction fee mechanism (TFM) is a triple (, , ) in which is a feasible allocation rule, is a payment rule, and is a burning rule.
-
A TFM (, , ) is individually rational if, for every history , total gas price paid by ’s creator is less or equal to the bid: .
-
A set of transactions is feasible if the total gas is at most the maximum block size .
How EIP-1559 mechanism works
-
Each transaction payment consists of two parts: base fee and tip.
-
Each block is associated with a base fee that is fixed by the history of past blocks and independent of the contents of the current block. Base fee r is determined by a specific function .
-
Each transaction specifies a tip , as well as a fee cap .
-
Based on these three parameters, the bid can be specified: . Note, that all the costs are determined per unit of gas.
-
Allocation rule: for each history and corresponding base fee , the allocation rule is to include a feasible subset of outstanding transactions that maximizes the sum of the gas-weighted bids, less the gas costs and total base fee paid. That is, for any , to maximize assigning 0 or 1 to subject to the block size constraint where is the transaction gas cost.
-
The payment rule transfers the difference between the bid and the base fee r to the block producer: for all and .
-
The burning rule burns the base fee: for all and . This rule was not defined in the general auction framework in the previous sections as it is EIP-1559-specific.
-
Block producer’s utility function:
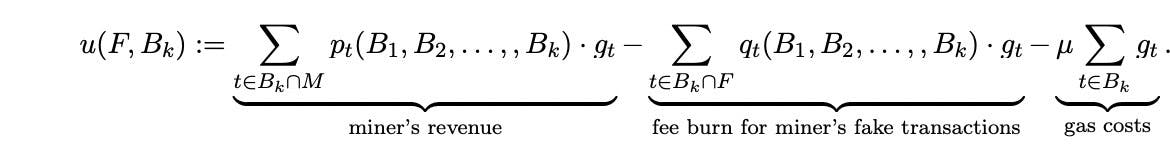
Formula source: the paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden.
The first term sums over only the real included transactions, as for fake transactions the payment goes from the miner to itself. The second term sums over only the fake transactions, as for real transactions the burn is paid by their creators (not the miner).
- We assume that a user bids in order to maximize its net gain (i.e., the value for inclusion minus the cost for inclusion). User’s utility function is defined by:
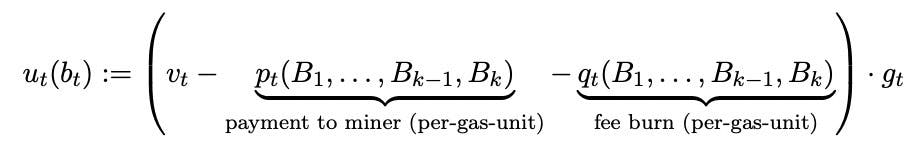
Formula source: the paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden.
Game-theoretical soundness analysis
Disclaimer: in this section, we assume that the block producer maximizes their revenue from current block without playing strategically. For the long term scale analysis, check section 7 of the paper.
Incentive-Compatibility from the block producer perspective
Incentive Compatible from block producer perspective means the block producer is incentivized to implement the intended allocation rule and disincentivized from including fake transactions.
In other words, the two properties should be satisfied: (i) excluding real transactions suggested by the allocation rule strictly decreases block producer utility, (ii) including fake transactions does not increase block producer utility.
-
A first-price auction (, , ) is incentive compatible as well. (the burning rule) is all-zero function as there are no burnings. Hence, payments equal bids and the block producer’s utility is maximized by the allocation rule.
-
The second-price auction (Vickrey Auction) is not incentive compatible as they can be manipulated via fake transactions. Consider a set of transactions that all have the same gas limit and a block that has room for three of them. In this setting, a Vickrey auction would prescribe including the three transactions with the highest bids and charging each of them (per unit of gas) the lowest of these three bids. Imagine that the top three bids are 10, 8, and 3. If a miner honestly executes a Vickrey auction, its revenue will be 3 × 3 = 9. If the block producer instead submits a fake transaction with bid 8 (so that the top three bids now are 10, 8, 8) and executes a Vickrey auction (with the top two real transactions included along with the fake transaction), its net revenue jumps to 2 × 8 = 16 (only two transactions are counted as in a fake transaction block producer pays to itself).
-
EIP-1559 mechanism is incentive-compatible if, for every on-chain history and mempool , a block producer maximizes its utility by creating no fake transactions and following the suggestion of the allocation rule x. Reorganize the block producer’s utility function:
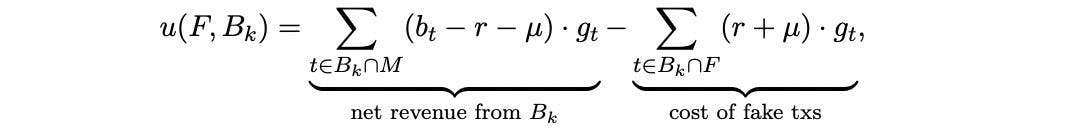
Formula source: the paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden.
Included fake transactions strictly increase the second term (by per unit of gas) while leaving the first unaffected. So, the block producer will only include real transactions. And when the second term is zero, the block producer’s utility is for any which is identical to the quantity maximized by the allocation rule . Thus, block producer utility is maximized by following the allocation rule.
If the base fee was paid to miners rather than burned, the EIP-1559 mechanism would only be µ-costly (instead of -costly) and fake transactions would be only mildly disincentivized.
Incentive-Compatibility from the user perspective (UIC)
Intuitively, UIC means that there is an “obvious optimal bid” when creating a new transaction. Obvious bidding should maximize a user’s utility as long as all the other users are also bidding in the obvious way.
The formal answer is described as the concept of a symmetric ex post Nash equilibrium (symmetric EPNE). Fix a TFM () and the on-chain history . A bidding strategy is a symmetric ex post Nash equilibrium (symmetric EPNE) if, for every mempool in which all transactions’ bids were set according to this strategy, and for every transaction with value , bidding maximizes the utility of ’s creator.
A TFM () is incentive-compatible for users (UIC) if, for every on-chain history , there is a symmetric EPNE.
-
First-price auction is not UIC. As the utility-maximizing bid depends on the precise numerical values of others’ bids, and not merely on the qualitative knowledge that they are following a particular bidding strategy. The same is true for the second-price auction.
-
The EIP-1559 mechanism is typically Incentive Compatible for Users, except in periods of rapidly increasing demand. We assume that a base fee r is excessively low for a mempool of transactions if the demand at price exceeds the maximum block size . The base fees become excessively low relative to blockspace demand spikes. That is, while demand can jump up quickly, fees will go up slowly as it is only 12.5% growth that can happen block over block.

Table source: the paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden.
When the base fee is excessively low, users must compete for scarce block space through their tips, and the 1559 mechanism effectively reverts back to a first-price auction, that is never UIC.
But whenever the base fee is not excessively low, there is an “obvious optimal bid” in the form of a symmetric EPNE. The allocation rule prescribes including precisely the transactions with . Because for all , these are precisely the transactions with . In particular, because is not excessively low for , this allocation is feasible.
There are two types of transactions t to consider, high-value () and low-value (). When all bids are set according the strategy , the high-value transactions are included while the low-value transactions are excluded. The utility of creator is () if t is a high-value transaction and 0 otherwise. Every alternative bid for a high-value transaction either has no effect on its creator’s utility (if ) or leads to t’s exclusion from the block (if ) and reduces this utility from to 0.
Every alternative bid for a low-value transaction either has no effect on its creator’s utility or leads to t’s inclusion in the block. The latter can only occur when , in which case the creator’s utility drops from 0 to . We conclude that there is no alternative bid for any transaction of that increases its creator’s utility.
Off-chain agreements (OCA)
For a feasible set of transactions and a block producer m, an off-chain agreement (OCA) between ’s creators and m specifies: (i) a bid vector , with indicating the bid to be submitted with the transaction , (ii) a per-gas-unit ETH transfer from the creator of each transaction to the block producer m.
In case of OCA, the user’s utility is defined by:
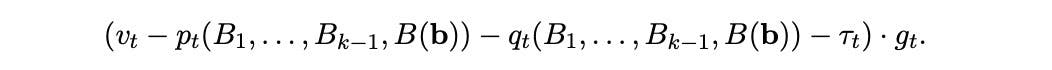
The block producer’s utility is defined by:
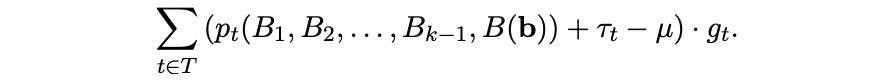
The joint utility of users and block producer is defined by:
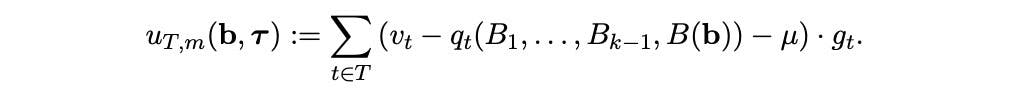
The point of an OCA is to maximize the joint utility. Using transfers, a miner and users can then split this joint utility among themselves in an arbitrary way. A TFM is OCA-proof if, for every OCA, there is an equally good on-chain outcome. In other words, if a TFM is not OCA-proof, there are scenarios in which a miner and users can collude to achieve higher joint utility — and, after defining appropriate transfers, higher individual utilities than in any on-chain outcome.
-
First-price auction is OCA-proof. Because (burning rule) is the all-zero function, the objective maximized by the allocation rule is identical to the joint utility. Thus, the joint utility of the on-chain outcome with bids cannot be improved upon by any OCA.
-
The 1559 Mechanism is OCA-Proof. Because is the constant function always equal to , the objective maximized by the allocation rule is identical to the joint utility. OCAs are the biggest game-theoretic driver for the why and the how of the fee burn in the transaction fee mechanism proposed in EIP-1559.
Thus, we ensured that EIP-1559 mechanism satisfies the three desirable game-theoretic guarantees for a transaction fee mechanism while the first-price auction (used for Ethereum fee pricing before EIP-1559) satisfies only some of the desirable properties.
Reading list: papers exploring auctions related to blockchain
-
Credible, Optimal Auctions via Blockchains by Tarun Chitra, Matheus V. X. Ferreira, and Kshitij Kulkarni.
-
CREDIBLE AUCTIONS: A TRILEMMA by MOHAMMAD AKBARPOUR and SHENGWU LI.
-
Credibility and Incentives in Gradual Dutch Auctions by Kshitij Kulkarni, Matheus V. X. Ferreira, and Tarun Chitra.
-
Optimal Strategic Mining Against Cryptographic Self-Selection in Proof-of-Stake by Matheus V.X. Ferreira, Ye Lin Sally Hahn, S. Matthew Weinberg, Catherine Yu.
-
Credible, Truthful, and Two-Round (Optimal) Auctions via Cryptographic Commitments by Matheus V. X. Ferreira, S. Matthew Weinberg.
-
Credible, Strategyproof, Optimal, and Bounded Expected-Round Single-Item Auctions for all Distributions by Meryem Essaidi, Matheus V. X. Ferreira, S. Matthew Weinberg.
-
Dynamic Posted-Price Mechanisms for the Blockchain Transaction Fee Market by Matheus V. X. Ferreira, Daniel J. Moroz, David C. Parkes, Mitchell Stern.
-
Proof-of-Stake Mining Games with Perfect Randomness by Matheus V. X. Ferreira, S. Matthew Weinberg.
-
Credible Decentralized Exchange Design via Verifiable Sequencing Rules by Matheus V. X. Ferreira, David C. Parkes.
Sources
-
zeroknowledge.fm Episode 269: Auctions with Kshitij Kulkarni, Matheus V. X. Ferreira and Tarun.
-
(AGT10E1) [Game Theory] Auction Theory by Selcuk Ozyurt.
-
(AGT11E1) [Game Theory] Mechanism Design by Selcuk Ozyurt.
-
The paper “Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559” by Tim Roughgarden.
Join us 💗
Explore open positions on our job board.
Follow us 🥁
Get the latest from Taiko:
-
Website: https://taiko.xyz.
-
Discord: https://discord.gg/taikoxyz.
-
GitHub: https://github.com/taikoxyz.
-
Twitter: https://twitter.com/taikoxyz.
-
Community forum: https://community.taiko.xyz.
-
Youtube: https://www.youtube.com/@taikoxyz.
Contribute 🤓
Contribute to Taiko on GitHub and earn a GitPOAP! You will also be featured as a contributor on our README. Get started with the contributing manual.